Los números binarios son la base de la tecnología digital y, como consecuencia, de las tecnologías de la información y la comunicación. Cualquier cosa que pasa por un sistema informático o de comunicación moderno, lo hace en forma digital. Esto es, la información (voz, video, audio, texto, etc.) acaba siempre siendo representaba con ceros y unos. Los ceros y unos son la base de los números binarios. Veamos qué son los números binarios y cómo se utilizan.
Los elementos electrónicos internos de los equipos digitales manejan la información en base a dos estados. Estos estados se representan de forma general como estado 0 y estado 1. No obstante, dependiendo del tipo de equipo de que se trate, cada uno de estos estados puede ser asociado con distinta característica física. Por ejemplo, en un determinado equipo, 0 voltios de tensión puede representar el estado 0 y 5 voltios el estado 1, mientras que en otro equipo, estos niveles pueden ser -3 y + 3 voltios, 1.200 y 2.400 hercios de frecuencia o luz y no luz en el caso de la fibra óptica. El hecho es que, independientemente de cómo se represente, siempre se manejan dos informaciones: 0 y 1. A estas informaciones se las conoce con el nombre de bit.
Los equipos electrónicos son capaces de manejar muy fácilmente estos bits y realizan con ellos todo tipo de operaciones a una gran velocidad. Los bits son fácilmente almacenados, transmitidos o cifrados. Se pueden hacer operaciones matemáticas complejas y representar con ellos todo tipo de información: números, textos, imágenes, sonido, vídeos, etc.

Sistema binario vs sistema decimal
La combinación de ceros y unos representan números. Son números iguales a los del sistema decimal que estamos acostumbrados a utilizar. El sistema decimal utiliza diez símbolos (del 0 al 9). Para seguir contando después del 9, se añade una cifra. Con dos cifras se puede contar del 10 al 99. Des esta forma se pueden ir añadiendo todas las cifras que sean necesarias.
El sistema binario utiliza dos símbolos (del 0 al 1). Para seguir contando después del 1, se añade una cifra (del 10 al 11). Al igual que en el caso del sistema decimal, se van añadiendo las cifras que se vayan necesitando.
El sistema decimal tiene base diez (utiliza diez símbolos) y el sistema binario tiene base dos (utiliza dos símbolos). Se pueden hacer sistemas de numeración con cualquier número de símbolos. En la historia hay ejemplos prácticos de ello. Por ejemplo, en informática es común la utilización del sistema hexadecimal (base 16, se representa por los números del 0 al 9 y las letras de la A a la F). La razón fundamental es que los números hexadecimales son cortos y pasar entre binario y hexadecimal es muy simple (cada 4 bits es un número hexadecimal).
En conclusión, el sistema decimal es el habitual para los humanos y el binario es el que utilizan las máquinas. Veamos cómo pasar de uno a otro.

Convertir de binario a decimal
Independientemente de que se disponga de dos o de diez símbolos, el hecho es que ambos sistemas pueden representar cualquier cantidad, por elevada que sea. Una misma cantidad, incluso con decimales, se puede representar tanto en base dos como en base diez.
Para entender cómo funciona un sistema de numeración, prestemos atención a lo siguiente: el número 43 es cuatro veces 10 más tres veces 1. De la misma forma, el número 5.243 es cinco veces 1.000 (103) más dos veces 100 (102) más cuatro veces 10 (101) más tres veces 1 (100). O lo que es lo mismo:
5.243 = 5·103 + 2·102 + 4·101 + 3·100 = 5.243 (en decimal)
Como vemos, cada cifra se multiplica por el número de la base (10 en este caso) elevado a la posición que ocupa la cifra (0 para la primera, 1 para la segunda, etc.). Por cierto, cualquier número elevado a cero nos da uno (100 = 1). Pue bien, con los números binarios ocurre exactamente lo mismo. El número binario 10110 es equivalente en decimal a:
10110 = 1·24 + 0·23 +1·22 + 1·21 + 0·20 = 22 (en decimal)
En los números decimales, cada cifra representa la cantidad de veces que se tiene 1, 10, 100, 1000, etc. En los números binarios, cada cifra representa la cantidad de veces que se tiene 1 (1 en decimal), 10 (2 en decimal), 100 (4 en decimal), 1000 (8 en decimal), etc. Dicho de otra forma, cada cifra de los números decimales es diez veces la anterior (100, 101, 102, etc.), mientras que cada cifra de los números binarios es dos veces la anterior (20, 21, 22, etc.).
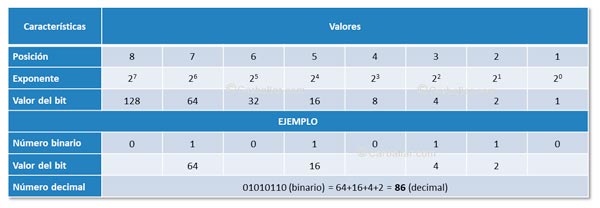
Por tanto, para convertir un número de binario a decimal sólo hay que fijarse en la posición que ocupan sus cifras con valor 1 y sumar sus valores correspondientes. Por ejemplo:
1101000 = 1·26+1·25+0·24+1·23+0·22+0·21+0·20= 64+32+8 = 104 (en decimal)
10110101 = 1·27+0·26+1·25+1·24+0·23+1·22+0·21+1·20= 128+32+16+4+1 = 181 (en decimal)
11111111 = 1·27+1·26+1·25+1·24+1·23+1·22+1·21+1·20= 128+64+32+16+8+4+2+1 = 255 (en decimal)
Convertir de decimal a binario
Una forma simple de convertir un número decimal a binario es teniendo presente la serie de números 1, 2, 4, 8, 16, 32, 64, 128, etc. A continuación se identifica el mayor número de esta serie que es menor o igual al número a convertir. Se anota la correspondiente cifra binaria, se le resta al número en cuestión y con la diferencia se vuelve a repetir la operación anterior hasta que el valor de la diferencia sea 0.
Por ejemplo, en el caso del número decimal 104, el mayor valor de la serie que es menor o igual es 64 (en binario 1000000). Si hacemos la resta 104 menos 64 obtenemos 40. El mayor valor de la serie para 40 es 32 (en binario 100000). 40 menos 32 es 8. El mayor valor de la serie para 8 es 8 (en binario 1000) y el resto es cero. Por tanto, el número binario resultante es 1000000 más 100000 más 1000, o lo que es lo mismo: 1101000.
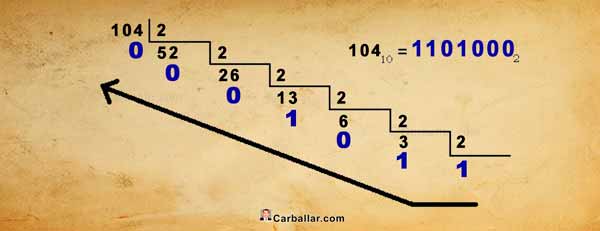
Otro procedimiento consiste en dividir por dos el número en base diez (sin sacar cifras decimales) e ir anotando el resto hasta que el cociente (el resultado de la división) sea cero. Al final, el número binario equivalente es el resultado de colocar los restos de las divisiones en orden inverso. En el caso del número 104 se haría de la siguiente manera:
104 / 2 = 52 y resto 0
52 / 2 = 26 y resto 0
26 / 2 = 13 y resto 0
13 / 2 = 6 y resto 1
6 / 2 = 3 y resto 0
3 / 2 = 1 y resto 1
1 / 2 = 0 y resto 1
El número binario equivalente es, por tanto, 1101000.
Quizás la forma más sencilla de convertir los números binarios en decimales y viceversa es utilizando un buscador. Simplemente hay que introducir, por ejemplo, ‘104 en binario’.
Por último, también se puede utilizar la calculadora científica que viene incluida en todos los sistemas operativos (Windows, Android, iOS, etc.). Se introduce el número decimal que se desea convertir y al seleccionar la opción binario (Bin), se verá su correspondencia en binario.
Representación binaria de un texto
Bien, parece que hay una relación directa entre número binarios y decimales pero, ¿Qué pasa cuando lo que se quiere representar son letras?. La respuesta es sencilla, a cada letra se le asigna una combinación de ceros y unos. Por ejemplo, la letra A se representa con 1000001, la B con 1000010, etc.
La primera vez que se presentó este problema fue en la época del télex. Las compañías de telégrafo necesitaban utilizar un sistema estándar que les permitiera transmitir mensajes a través del telégrafo. Finalmente, en el año 1963, el Comité Estadounidense de Estándares constituyó el código ASCII (American Standard Code for Information Interchange, en español, código estándar estadounidense para el Intercambio de Información). Este código ha evolucionado con el tiempo, pero es uno de los principales sistemas en los que se ha basado la tecnología informática.
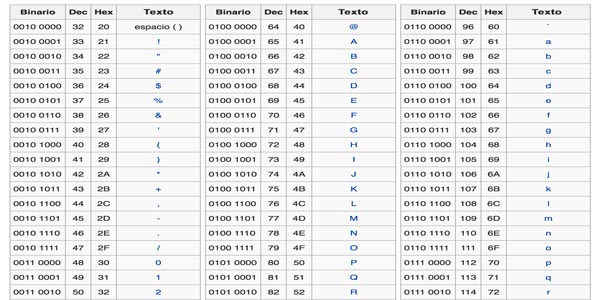
Por ejemplo, en el código ASCII de 8 bits (cada carácter ocupa 8 bits), esta serie de ceros y unos representa el mensaje Hola:
01001000011011110110110001100001
Si, además del carácter concreto, es necesario identificar también el estilo de letra, el color o el tamaño. Para ello, a los bits que identifican cada letra hay que añadirles aquellos otros que identifican el resto de características. Esta información adicional suele estar definida por cada aplicación o formato de archivo que se utilice.
Representación binaria del audio
Para digitalizar el audio se toman repetidas muestras de la amplitud de la señal analógica del audio, se cuantifican (se mide la amplitud concreta de cada muestra) y se convierte cada muestra en una secuencia de bits que la representa. La señal digital se puede almacenar o transmitir. Cuando se desea escuchar el audio o reproducir en destino, se toma cada secuencia de bits de cada muestra y se va reproduciendo la amplitud de la señal de audio.
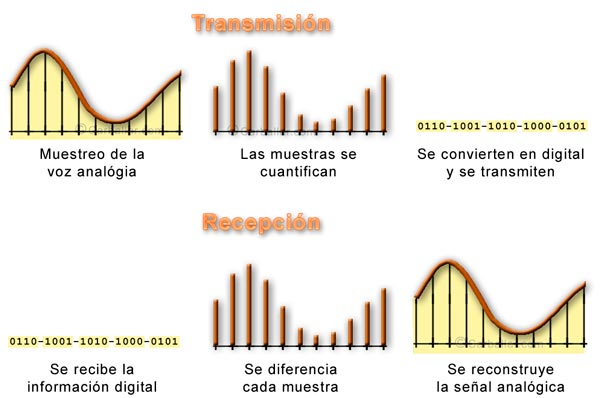
Esta es la forma simple de explicar el proceso de digitalización del audio. No obstante, si se aplicara esta técnica tal cual, una señal de audio telefónico necesitaría un ancho de banda mínimo de 64 kbps. En la práctica real, se busca que este ancho de banda sea el menor posible. Para ello, se llevan a cabo determinados procesos de codificación de la secuencia de bits resultante. Con esto se consigue que un mismo sonido, ocupe un espacio mucho menor, tanto para la transmisión como para el almacenaje.
Si le interesa conoce más sobre estas técnicas, puede consultar el artículo: Técnicas de codificación de la voz
Representación binaria del vídeo
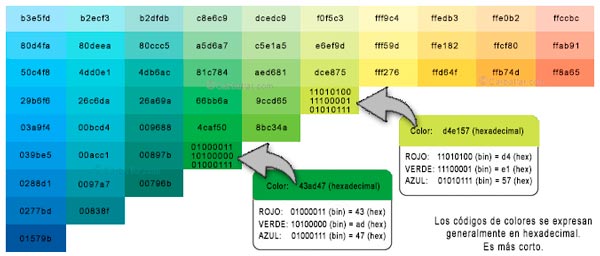
La representación binaria de las imágenes de vídeo consiste en digitalizar cada imagen de la secuencia de vídeo e irla reproduciendo a la velocidad deseada. Como sabemos, cada imagen está representada por un conjunto de puntos (conocidos como pixel). Cada punto tiene un determinado color. El color de este punto se representa por un número digital. El número de bits necesario para representar cada punto depende del número de colores que tenga la imagen.
Por ejemplo, si nuestra imagen tiene solo 4 colores, se podrían utilizar dos bits por píxel. Por ejemplo:
00 verde
01 rojo
10 azul
11 blanco
Si la imagen fuera de 20×10 píxeles, como cada pixel ocupa 2 bits, el tamaño de cada imagen sería de 20·10·2=400 bits. Con este sistema del ejemplo, una imagen completamente verde sería una secuencia de 400 bits 0. Los vídeos se suelen reproducir a 25 imágenes por segundo. En nuestro caso, esto supondría un ancho de banda de 400·25 = 10.000 bps (bits por segundo). Dicho de otra forma, un minuto de vídeo ocuparía 600.000 bits.
Las imágenes de vídeo no suelen tener 4 colores, sino miles de ellos. Por otro lado, el tamaño de la imagen depende de la resolución de la misma. Las imágenes HD suelen ser de 1280 x 720 píxeles, las de Full HD de 1920 x 1080 píxeles y la resolución de una Ultra HD o 4K es de 3840 x 2160 píxeles. Si hacemos cuentas, el ancho de banda necesario para transmitir un minuto de vídeo sería muy grande. Al igual que con el audio, para reducir este ancho de banda se utilizan técnicas de codificación.
En cualquier caso, lo que tenemos es que las imágenes de video se pueden representar digitalmente con cierta facilidad.
Conclusiones
Aunque las personas recibimos la información en forma de letras, sonidos, imágenes o movimiento, esta información es manejada y almacenada por los sistemas informáticos en forma de 0 y 1.
Cualquier tipo de información se puede representar de forma binaria. Para ello, se suelen utilizar técnicas de codificación que hacen corresponder cada unidad de información con una combinación de ceros y unos. Una vez digitalizada se puede guardar la información, tratarla digitalmente o transmitirla. Para representar de nuevo la información en su estado natural solo hay que revertir el proceso de codificación.
El sistema de numeración binario se utiliza para representar las informaciones, así como realizar todo tipo de operaciones con ellas: modificarlas, almacenarlas o transmitirlas. Incluso, utilizando técnicas de inteligencia artificial, se pueden interpretar estas informaciones y tomar decisiones de forma automática en base a ello.
La digitalización resulta fundamental para el desarrollo de todo tipo de tecnologías. No solo se está digitalizando todo, sino que cada vez hay más aplicaciones que lo analizan todo de forma automática. La base de todo ello son los números binarios.
Más información
Aquí se ha expuesto de forma resumida qué son los números binarios y cómo se utilizan en el mundo informatizado actual. En este blog se dispone de muchos otros contenidos relacionados. Por favor, utilice el buscador de contenidos que tenemos en la cabecera de este blog.
Estos son algunos otros artículos que pueden ser de interés:
- Qué es el cifrado de datos y para qué sirve
- La tecnología de Google Earth
- Qué significa Big Data, para curiosos
REF: FW-PG60
